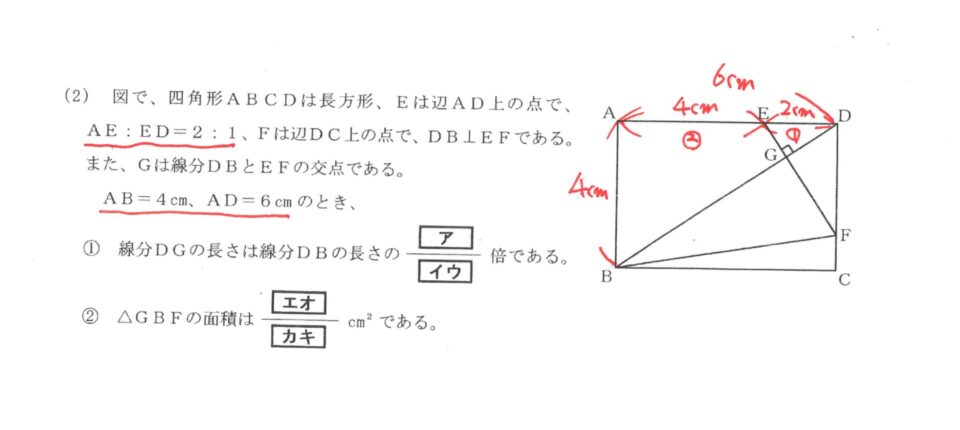
まず与えられた条件を確認します。
四角形ABCDは長方形→4つの角がすべて90°、向かい合う辺が平行
AB:ED=2:1→図に書き込みます。
DB⊥EF→図にすでに書いてあります。∠DGE=90°は三平方の定理、相似などに使う可能性があります。
AB=4㎝、AD=6㎝→図に書き込みます。センチメートルは省いてもいいですが、比の数字と区別するため、比の数字を〇や□などで囲み実際の長さを区別します。
また、AB=4㎝と与えられたので、AE=4㎝、ED=2㎝とわかるので、これも書いておきます。
これで準備ができました。
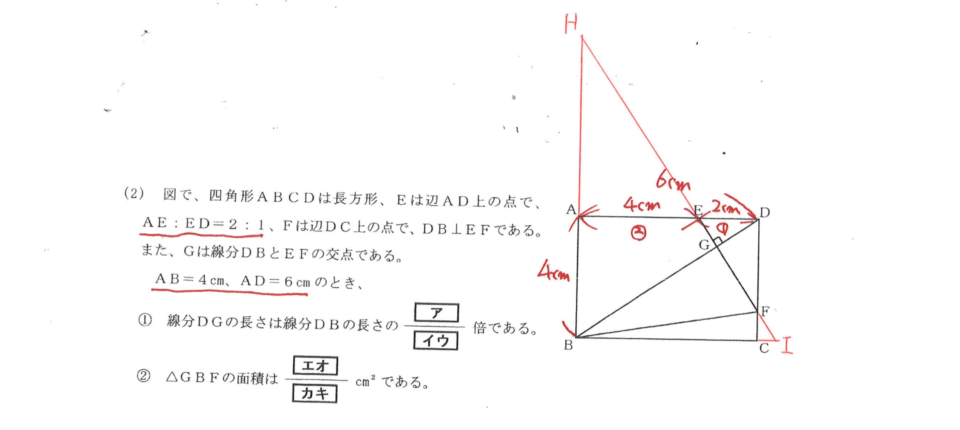
①から解いていきます。
DGの長さを求めなさいという問題ですが、愛知県の入試問題での解き方の定番としては、DGを辺となる三角形の相似を利用して長さを求めるというものです。
どの三角形の相似を利用するかというと、
①上の補助線を書き、△DGF∽△BGHを利用する方法
②右に補助線を書き、△DGE∽△BGIを利用する方法
の2通りの方法があります。
この方法は愛知県の図形の問題を解くときに非常によく使う方法なのですが、今回の問題にはどちらも使えません。
何故かというと、点Fの位置が決まっていないため、①の場合だとAHの長さ、②の場合だとCIの長さが求められないからです。
②を解くときにDFの長さを出すので、まずDFの長さを出してから相似を使うということもできますが、回り道になりますので、今回は別の方法で解きます。
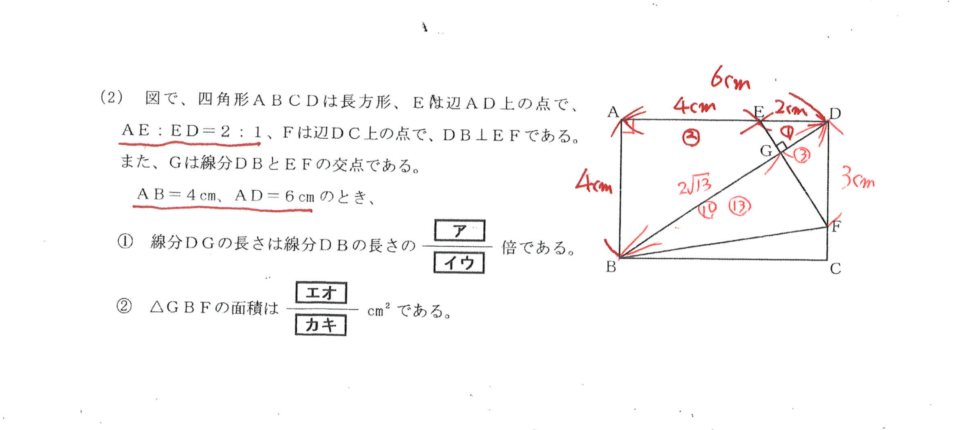
では、どこに注目して解けばいいのでしょうか?
ここでは、△DGEと△DABが相似であることを利用して解くのがいいと思います。
△DGEと△DABは、∠DGE=∠DAB=90°、∠EDG=∠BDA(共通)から2組の角がそれぞれ等しいため相似になります。
鉄則4 1つの角を共有する2つの直角三角形は相似になる
DG=xとおいて、対応する辺の長さの比が等しいことを利用して出したいところなのですが、DEに対応するDBの長さがわかりません。
そこで△ABDで三平方の定理を利用して、DBの長さを求めておきます。
\(D B^{2}=4^{2}+6^{2}\)
\(D B= \pm \sqrt{52}= \pm 2 \sqrt{13}, \)
\(D B>0 \text { なので、 } D B=2 \sqrt{13}\)
次に線分DGの長さを求めます。
△DGE∽△DABより
\(
\begin{aligned}
D E: D B & =D G: D A \\
2: 2 \sqrt{13} & =D G: 6 \\
1: \sqrt{13} & =D G: 6 \\
D G & =\frac{6}{\sqrt{13}}=\frac{6 \sqrt{13}}{13} \\
D G \div D B & =\frac{6 \sqrt{13}}{13} \div 2 \sqrt{13}=\frac{6 \sqrt{13}}{13} \times \frac{1}{2 \sqrt{13}}=\frac{3}{13}
\end{aligned}
\)
これで線分DGと線分DBの比が出せました。
次に②の△BGFの面積を求めます。
①で線分BGの長さをすでに出していて、∠BGF=90°なので、線分GFの長さがわかれば、△BGFの面積を直接求められそうです。
しかし、線分GFの長さを出すのに計算が多くて苦労しそうです。
そこで、①で出した答えを利用して求めます。
①でDG:DB=3:13と出しました。
そこから△DGF:△DBF=3:13 ということがわかります。
鉄則5 高さが等しい三角形では、底辺の比と面積の比が等しくなる
△DBFの面積はすぐに出せます。
3×6÷2=9
△DGF:△DBF=3:13より、△DGFの面積は、
\(9 \times \frac{3}{13}=\frac{27}{13}\)
となります。

